YouTube Book Reveiws

Rationale: I need to know what books I've reviewed on YouTube.
[Update 1/2/23: really, I was about to do a review for one of these.]

Below is a catalog of those reviews and an Amazon link to the book. The text link above the Amazon link is a link to the review video flip through. I may try to integrate text book reiviews later.

I have categorized these into non-exculsive sets of either (1) Topics and (2) Book Series. All books in the second set appear in at least one topic, and some books appear in multiple topics. At some point I'll probably say why I included these particular series (that is, why I like them).

---

The Frontiers Collection

Schlosshauer, Maximillian, Dechoherence and the Quantum to Classical Transition

Petkov, V Relativity and The Nature of Spacetime

Zeh, H.D. The Physical Basis of the Direction of Time

---

General Physics/Physics Surveys

Leonhardt and Philbin Geometry and Light	Moore, Thomas Six Ideas That Shaped Physics: Unit C: Conservation Laws	Moore, Thomas Six Ideas That Shaped Physics: Unit N: Lawas of Physics are Universal	Zeh, H.D. The Physical Basis of the Direction of Time
Padmanabhan Sleeping Beauties in Theoretical Physics	Schwartz, M. Principles of Electrodynamics	Lemons, Don Perfect Form

---

Relativity

Lawden, D.F. Introduction to Tensor Calculus, Relativity and Cosmology

Petkov, V Relativity and The Nature of Spacetime

Will, Clifford Theory and Experiment in Graviational Physics

---

Quantum Mechanics

Ahronov and Rohrlick, Qunatum Paradoxes	Basdevant and Dalibard, The Quantum Mechanics Solver	Schlosshauer, Maximillian, Dechoherence and the Quantum to Classical Transition	Cohen, David W., An Introduction to Hilbert Space and Quantum Logic
Norsen, Travis Foundations of Quantum Mechanics	Sakurai, J.J. Modern Quantum Mechanics	Sudbery, A. Quantum Mechnicas and the Particles of Nature	Tomonaga, S.-I. The Story of Spin

---

Statistical Physics

Ben-Naim, Arieh Entropy and the Second Law

Ben Naim, Arieh Entropy Demystified

Krauth, W. Statistical Mechanics: Algorithms and Computation

---

Applied Phyiscs and Engineering

Feynman, Richard The Feynman Lectures on Compuation	Hubert and Schaefer, Magnetic Domains	Coleman, Charles Modern Physics for Semiconductor Science
	Szirtes, Thomas, Applied Dimensional Analysis and Modeling

---

Mathematics

Farlow, Stanley Partial Differential Equations for Scientists and Engineers

Gardiner, Anthony Understanding Infinity

Cohen, David W. An Introduction to Hilbert Space and Quantum Logic

Tapp, K Matrix Groups for Undergraduates

---

Mechanics

---

Dover Books

Farlow, Stanley Partial Differential Equations for Scientists and Engineers	Gardiner, Anthony Understanding Infinity	Leonhardt and Philbin Geometry and Light	Lawden, D.F. Introduction to Tensor Calculus, Relativity and Cosmology
Schwartz, M. Principles of Electrodynamics

---

Lecture Notes in Physics

Padmanabhan Sleeping Beauties in Theoretical Physics

Norsen, Travis Foundations of Quantum Mechanics

---

Multiversal Journeys

---

Student Mathematical Library

---

Oxford Master Series

Answering Aristotle - Index

I am reading Aristotle's Physics, and as I do with non-technical books, I try to write a topic sentence (here, "summary") for each section. The "chapters" in Aristotle are approximately the size of a good section. This is a list of those sentences. The chapter links, however, have me doing something different: when Aristotle makes assertions or predictions, and where I think that contemporary physics has something to say about them, I try to make some notes about that.

Book I

Chapter	Summary
I.1	Although understanding something means we can reason from first principles, discovering these principles requires us to sort them out from the aggregate observations we are built to apprehend.
I.2	There must be more than one thing because the ways in which all reality can be made of one thing each require there to be multiple things.
I.3	The definition of a whole cannot be found in the definition of its parts, so that things exist does not mean that there is an existence that they are a part of.
I.4	The number of kinds of things must be finite since the infinite is unknowable and a finite body cannot be composed of an infinite number of finite bodies.
I.5	All principles must be opposites that admit admixtures of opposites, and the properties of an object may consist of combinations of these principles.
I.6
I.7
I.8
I.9
I.10

Book II

Book III

Book IV

Book V

Book VI

Book VII

Book VIII

Answering Aristotle I.4 - There Cannot Be an Infinite Number of Things

← Previous ( Physics I.3 )

Answering Aristotle

( Physics I.5 ) Next →

---

Physics I.4 The number of kinds of things must be finite since the infinite is unknowable and a finite body cannot be composed of an infinite number of finite bodies.

Again Aristotle is arguing against someone to prove his point. In this case, Anaxagoras. Aristotle presents this as since "it is impossible for something to come into being from non-being," so everything that exists is made up of smaller constituents. And if everything comes from smaller constituents, then there cannot be a smallest object -- it, itself, would need to be composed of even smaller things. Aristotle, disagrees. Although there must be more than one thing, or even one kind of thing, there cannot be an infinite number of things, let alone an infinite number of kinds of things that the finite things we see are composed of.

It is a little difficult to keep track of things here, because sometimes Aristotle seems to be talking about the number of things that exist; at other times, he seems to being talking about the the number of kinds of things that exist; and at still other times, he seems to be arguing about the number of different properties that a thing can hold.

Aristotle's argument that there cannot be an infinite number of things has five parts, of different quality:

(1) The infinite is unknowable.

This is rather technical in the sense that it makes a strong point about the limitations of what we can perceive in thought. However, it is not really true that "if an object consists of an infinite number of things and forms, its nature is unknowable." This is a little strong, since something that consists of an infinite regularity could be understood in principle without apprehending its nature as a whole. That is in fact what we do in science. We don't perceive the entire array of atoms in a crystal lattice. For the most common measurements of the lattice, from X-ray diffraction, we don't even directly look at the regular array. Instead, we look at the regularities in the array of atoms making up a sample, and learn about its constituents that way.

(2) If an object has a finite size, then its parts must also be finite.

Zeno would be proud. This is a classic piece of the Dichotomy. However, Aristotle didn't buy Zeno's paradoxes any more than we do. In fact, many of his reasons are good enough to refute Zeno in any but a pedantic way (today, even the pedants should understand these paradoxes are refuted even at the more fundamental levels*). The parts of a homoeomerous substances could be made of ever smaller parts if you take a continuum model or even an infinitesimal model of matter.

(3) That some of every constituent is present in every object is inconsistent.

The best way I can present this argument is that if an object has a finite number of (kinds of) constituents, and if those constituents are differentiated and their relative preponderance determines the object's nature, then at some point when you reduce the size of a sample below a certain volume, you will have a sample of the object with an insufficient amount of one of its constituents to be the same kind of thing as it reduces in size. The divided objects cease to be of the kind of the original object. This would be equally true with random fluctuations in small samples.

(4) Nothing material can be extracted from the smallest instance of a substance.

Once you reach the limit above, you cannot make a smaller copy of the thing you're dividing. This is a direct response to Anaxagoras.

(5) An infinite collection must be both divided and connected simultaneously.

The infinite number of things that Aristotle is talking about are the constituents of other things.

Now that I try to explain them, I don't think any of them are very good. I think many of the reasons he discussed earlier are much better than his discussion here, but the conculsions he came to were wrong. And ironically, on this one Aristotle is right.

Nothing is composed of an infinite number of things, to our knowledge.[2] It seems like there are a finite number of kinds of things that something can be composed of at the smallest level (standard model) and even a finite number of possible elements something can be made of (periodic table). So although a copper ball has an impossible number of atoms in it (maybe 10²⁵ or so), it is still a finite number, and although the atoms that make up the ball have constituents, they have a small number of constituents (say, around 250).

____________________________
[1] Although, as philosophers, they do continue to find value in them. See Salmon, Zeno's Paradoxes and Sainsbury, Pardoxes. [Amazon]

[2] But there could be preons inside of quarks (but probably not). And if there are preons inside of quarks, then what's inside the preon?

---

← Previous ( Physics I.3 )

Answering Aristotle

( Physics I.5 ) Next →

The Two Ockham's

In reading the first chapter of Bostrom's Anthropic Bias: Observation Selection Effects in Science and Philosophy,[1] his overview dealing with multiple worlds makes me feel as if there are two ways in which Ockham's Razor[2] are being used in science. That is, the general maxim of reducing the number of "entities" to a minimum is applied in two opposing ways, one of which is evident in anthropic reasoning. One of these ways is to reduce the number of actual things that you suppose to exist and the other is to reduce the number of postulates required to make predictions with a theory.

How does that work?

Fine tuning is a modern sin in theoretical physics. A theory that has a large number of free parameters, but only a few of which could lead to observed consequences, needs to have additional assumptions about those parameters. If these are unexplained, then the theory is fine tuned. This is generally felt to be a flaw because it is surprising that an otherwise successful theory should require a large number of ancillary assumptions -- 31 in the case of particle astrophysics[3] -- to predict the existence of the universe. Although not strictly a error, taking an elegant and insightful theory and clothing it in hand-me-down experimental parameters is a bit gauche.

This is where the anthropic principle comes in. This principle, in this case, states that the universe has to be the kind of universe where you and me can exist. We're pretty sure that we do. This constrains overly loose theories, theories that require fine tuning, so that they can make predictions. This method was famously used by Steven Weinberg to predict the approximate magnitude of the cosmological constant. This has also recently been used to try to shore up string theory as it has become looser, parameter-wise, than once thought. Anthropic reasoning is an end around fine tuning.

The expansion of possible string theories from five to an infinite number has made anthropic arguments possible in that each particular universe that would be associated with a string theory[4] (with different parameters) exists, and the reason why we are in this universe with these fundamental constants is not because of any finely tuned assumptions that we have to make, but rather it is because of the existing universes, we have to be in a universe that supports our existence. This can be true with parallel universes, sequential universes, and so on, just as long as there is an infinite reservoir and the proportion of those universes is a subset of the same transfinite cardinality of the reservoir.

This is what brings me to Ockham's razor. This is usually stated as "entities must not be multiplied beyond necessity" or "plurality should not be posited without necessity." If there is no necessity to postulate a soul in order to understand consciousness, then don't postulate a soul. Normally, you would think that this would exclude a string theory landscape, that in order to explain the values of the universal constants that we measure, we need to postulate not just a soul, but an infinite number of souls.

But that's just one way to think about it. Another one is Aquinas' maxim, "It is superfluous to suppose that which can be accounted for by a few principles has been produced by many." In this case, the anthropic principle is supported by Ockham's razor. We have literally reduced the number of assumptions we need to make from 31 ad hoc interpretations of experiments to a single proven principle.

Both cases have a claim to be following the spirit of Ockham, and to me neither is obviously right. At least, neither seems to be the better argument in all cases. So, we have a situation where the same, admittedly somewhat subjective[5], principle would require us to take opposite approaches to the same problem. How do we decide which to follow?

_____________________
[1] Anthropic Bias: Observation Selection Effects in Science and Philosophy, Nick Bostrom. [Amazon]

[2] I prefer the ckh over the cc. How can Occam's Razor be named for Isaac of Ockham?

[3] See for example Tegmark, Aguirre, Rees, and Wilczek's "Dimensionless Constants, Cosmology and Other Dark Matters." [arXiv] See also Physics Frontiers 55: Multiversality.

[4] Anthropic Landscape of String Theory, Leonard Susskind. Extrad Dimensions in Space and Time [Amazon], Bars and Terning, Multiversal Journeys Series. See also: Physics Frontiers 35: The String Theory Landscape.

[5] But Ockham's razor is no less subjective than the beauty of a physical theory, and a lot of people give that a lot of weight.

Answering Aristotle I.3 - There Is More than One Thing II

← Previous ( Physics I.2 )

Answering Aristotle

( Physics I.4 ) Next →

---

Physics I.3 The definition of a whole cannot be found in the definition of its parts, so that things exist does not mean that there is an existence that they are a part of.

This reminds me of my first encounter with Aristotle, which happened to be when I was taking a graph theory course as an undergraduate. In the Posterior Analytics, Aristotle propounded that an argument that had to be made case by case wasn't a true derivation, or "...we often fall into error because our conclusion is not in fact...universal in the sense we thing we prove it so." When we prove a proposition case-by-case, instance-by-instance, "then the the demonstrations will be true of the individual instances...and will hold in every instance of it, yet the demonstration will not be true of this subject commensurately and universally." Aristotle's example, as so many it the text, is geometric: if the proof is shown for isosceles, scalene, and equilateral triangles, or if it is true of acute, right, and obtuse angles, then even though it is true for every triangle or for every angle, it is not true of triangles themselves because the proof does not follow from the nature of the triangle.

Aristotle always seems to say that kind of thing.

There is something reasonable about this. If there is a property of an object or a situation, then it should be derivable from the qualities of the object. If you need to bring in other conditions, then maybe it's the combination that has the property. Humans don't look like bushes, but humans wearing camouflage clothes and makeup can. The property of bush-likeness is a property of the clothing, not the man. Furthermore, I could create a situation where I found tofu dishes everyone likes: some people like tofu hot dogs, some people like tofutti, and even I like gelatinous tofu with beef in a szechwan sauce. However, people don't like the tofu, they like the flavorings around the tofu. Very few people eat plain dehydrated tofu bars.

But remember, as I was reading this, I was taking a graph theory course. It was taught by the math department, but the course was a required course computer science majors, but it did use proofs.* Proof courses often had themes that were not explicit in the content, techniques for proofs that are useful in the field. For probability theory, it was condition and uncondition. For graph theory, proof by cases. For example, if you can prove that a process works for all even number cases, then you can do the same for all odd number cases, then you can say the process works for all cases. This was even true of the four color theorem, which I think we will all say is a property of maps -- it is not a different property for different kinds of maps.

So I think that Aristotle has a point, but he's taken it a little too far: proof through cases, if you can demonstrate that you have exhausted all the cases, can still show that a derived property is a property of the system.

Some of what Aristotle is saying in I.3 has a similar feel.**

Unfortunately, that feel is very hard to follow. Aristotle talks about qualities like "paleness" as if paleness is to humans as quarks are to protons, and he does so with the object to show that there must be more than one thing. He does so mostly while arguing against positions that aren't clearly defined, so it feels like he's not arguing directly -- but since he doesn't restate the positions he is attacking.

Here Aristotle feels he has successfully defended against two propositions:

(1) Non-being has being.

(2) There exist indivisible magnitudes.

both of which have some merit, today.(*3) That non-being might have being means something like that the vacuum has some properties, but today we think that gravity is the theory of space-time, that mass can bend its fabric. Furthermore, quantum gravity is an attempt to find the quantum mechanical properties of this fabric. We think that this is true. The second is the atomic hypothesis, which wouldn't be accepted until the late 19th century, and today the standard model is full of indivisible, but not immutable, magnitudes.

____________________________________
* "Pure math" courses are proof-based somewhat like high school geometry, they aren't the endless calculations of algebra and calculus classes. You are expected to demonstrate that something works, or is a kind of mathematical tool, using logic. When the courses were required for other majors, computer science and math ed., they ended up being very, very simple.

** I thought I would give an example here of Aristotle saying something similar in I.3 as I quoted in the Posterior Analytics, but the prose is quite convoluted, and the long, ellipsis-laden quotes I can find in the Physics say almost the same thing.

(*3) Giving examples like this and those I did in I.2 are not what I wanted to be doing here.

---

← Previous ( Physics I.2 )

Answering Aristotle

( Physics I.4 ) Next →

Geometric Irony

This morning on my drive to work, I was listening to an old (May 2018) episode of Conversations with Tyler, the second half of which was a discussion between Nassim Nicholas Taleb and Bryan Caplan on the problems with education. The recurrent examples of these problems are poetry and geometry, at least one of which probably scares you. Their issue wasn't that there's anything inherently wrong with poetry and geometry, in fact they think that both are perfectly good hobbies that everyone should have (Taleb, I should say, was a little more tolerant of your poetry classes, but not that much). But they worry about the practical problem that very few students will pursue a career in them, and students graduate from school at eighteen or twenty-two having forgotten approximately 100% of the poetry and geometry that they "learned"¹ in class and having no idea what kind of career will suit them. There aren't many poets in the world, and there are even fewer that have learned to convert verse into cash with ab efficacy sufficient to fill a refrigerator. And what fifteen year olds need to do is to sample the possibilities of how they can fit into the world, like plumbing and customer service.²

The liberal arts are best left to Sunday afternoons on the porch and autumn walks in the park.

I had finished the first half (where Tyler Cowen interviewed Taleb) and started on the part where Taleb talked with Caplan about his book The Case Against Education (both segments included a lot of talk about Taleb's books, especially Antifragile),⁴ when it was time to stop and get my cup of coffee.² I pulled out a paper on the history of the renormalization group and a pad of Bristol board, and started the day off by working on a cartoon for class and a bikini girl for Instagram while waiting for the caffine to get me attentive enough to read an academic paper. While I was drawing the cartoon, which is about integrating to find a volume, a local antique dealer, J., came by and we talked about finding volumes a little bit.

The cartoon, I hope you can see,⁵ shows the Riemannian process behind the integral for finding the volume of the pyramid. J. saw the point right away ("what about the steps?"), and pulled out a problem for his store. The way he'd have to solve the problem was, he said, to weigh a stick of butter, then to carve a scale model out of it, weigh again, and then do some ratios. This is a very good method.⁶

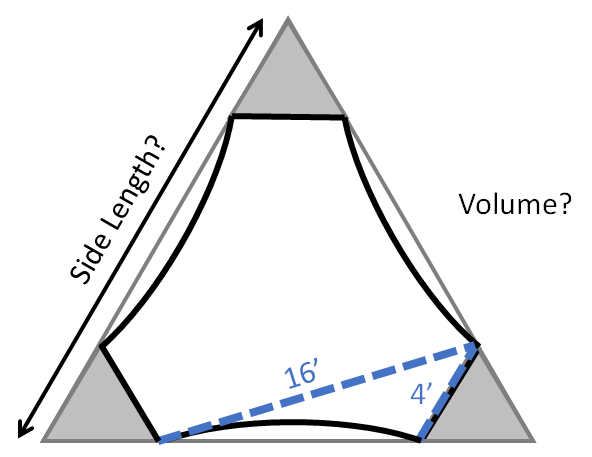
When he was in Versailles and saw a structure whose somewhat triangular shape he wanted to reproduce for his store, where he would put featured paintings at one point, antiquities on another, and books on the third. The shape was an equilateral triangle with the tips cut off (so, a hexagon), where the long edges had a slight inward curve. He'd add some walls and french doors as well, but what he wanted to know is that if the distance between next nearest points was 16' and the size of the cut was 4', what is the volume of concrete required to build the 1' thick base of the structure? I calculated it out with a little geometry, the quadratic formula, and a rather annoying bit of vector calculus (which was overkill).⁷ Then C., the old Airforce master sergeant, came by and we talked about history books and historical novels until the larger group started coming in. J. took the sketch and calculation, I went back to drawing, and some girls sat behind me watching me draw the leopard print on the pinup's bikini.

Then, when I got back into my car to get to work, I listened to the next fifteen minutes of the discussion, where Bryan Caplan and Nassim Nicholas Taleb continued their discussion on how unlikely it was that you'd end up using things like geometry or art in your day to day life, and thought about the wisdom of their words.

______________________________
¹ In fact, students lose the factoids they memorize for high school and undergraduate texts with a half life of about two weeks. So they'll always "remember" something from your class.

However, it might be the wrong thing. I remember talking to a high school friend just a year or two after graduation who was sure that Lamrkian evolution was correct, because he'd read it in the HS biology textbook. He even remembered the specific example: proto-giraffe mommies stretched their necks to reach higher leaves, and so their babies had longer necks. And then this repeated over generations until giraffes were the long necked freaks of nature we see in zoos today. This was in fact in the book (I remembered it, although I never studied in high school, so I don't know why), but it was there as a historical contrast to Darwinian evolution.

² And if you know me, especially if you knew me twenty years ago, you might remember my old rants against mindless education. And I still feel that way. I think, on the whole, Caplan and Taleb are correct. I'm not a fan of the pyramid schemes of psychology, but education kids love them, especially Maslow's heirarchy of needs. Poetry, art, and music are offerings to the sacraficial altar of self-actualization at the top of the pyramid. Caplan, and to a lesser extent Taleb, want the schools to focus more on the bottom steps of the pyramid, helping kids build the skills to keep themselves fed, housed, and safe. Those are the fertile soil for spiritual growth.

On the other hand, whenever I hear someone say "it would be better to teach kids EXCEL instead of calculus," I think, "You have to do the calculus before you use EXCEL."

^2½If you're cool, then you know Iggy Pop's feelings are also in tune with Caplan and Taleb from reading his liner notes on the reissue of Raw Power (which I did, of course).

...if you both like Iggy Pop and are literate (which I do and am, of course), which is not guaranteed (and that's the way he likes it; check out his liner notes).

³ I own a copy of Caplan's book and now I want a copy of Taleb's (I've read two others), but I'm about 40 books behind over the course of the pandemic. I usually read at least 50 books a year, but have gone down to a little over 30 each in 2020 and 2021.

⁴ I have a long commute which interacts with a complex morning routine, so this is a very simplified version. I've discussed the jalapeno boudin kolaches elsewhere.

⁵ Hopefully I'll get a way to put images up here.

I did! Ha! Although the screw ups on the cartoon make me nervous. I've spared you the pinup, which is beautiful, but you're not authorized for that kind of titillation. Bring a note to me during office hours from your psychiatrist saying that it's mentally safe for you to view such things, and I'll give you a link.

⁶ Before there was a lot of computer time available, and even when computers were reasonably slow, this was how experimentalists would do numerical integrations on their data. They'd plot out the spectrum on their plotter, very carefully cut out the shape of the specturm, and then weigh it. That weight would be compared with the weight of the paper and the untis on the axes to find the integral.

This is exactly J.'s butter technique.

⁷ If you are Nassim Nicholas Taleb and you really do enjoy doing geometry on your porch on Sunday afternoons, then this is a good little problem for you.

Answering Aristotle I.2 - There Is More Than One Thing I

← Previous ( Physics I.1 )

Answering Aristotle

( Physics I.3 ) Next →

---

Physics I.2 There must be more than one thing because the ways in which all reality can be made of one thing each require there to be multiple things.

Aristotle is agnostic about the kind of thing that is the one thing. Is it a substance, a property, an element?* It doesn't matter. If there is only one of them, then he asserts there will be a contradiction. Although most of his arguments are directed against Parmenides and Melissus, they are of a kind: find what seems to be a logical contradiction, e.g. the skinny man is fat, that comes from some assumptions. One that he asserts are that something cannot be finite and infinite at the same time.

These do not feel very compelling. For example,"...so there will be a substance as well as a quality, in which case it is twofold..." feels, at least in the translation, as if there is some confusion here. The two things are of such different kinds that I don't know how you can call them "two things," really.

What this brings to mind, though, is string theory. In the standard model of particle physics, you have a number of fields corresponding to two kinds of particle: bosons and fermions. The fermions are leptons (electrons) and quarks, which constitute matter. The bosons, photons, gluons, and W & Z particles, constitute the fundamental forces of nature (sans gravity), the connections between matter particles, in a way.

String theory makes all of these particles one kind of thing.

And because we can envision these particles as excitations in their corresponding fields. That is, whenever the electron field gains energy, a new electron is born. This is a little bit weird to think about in fundamental physics, because we don't have an independent concept of an electron field. But in condensed matter physics, we do have strong classical ideas about the meaning of some of the fields that appear in matter. We know about sound waves, we know about spin waves (magnetization waves). These waves are continuous and extend through the body. They have standing states, just like the standing waves on a string or a membrane that you might be able to envision.

And they're quantum mechanical.

The physics of these waves are describes as excitations in their corresponding fields. A spin wave is an excitation in the local magnetic polarization (magnetization) of a ferromagnet, and these excitations can only happen for certain multiples of a fundamental oscillation mode, just like the vibrating string. However, unlike the vibrating string,** there is a minimum energy necessary to excite a single vibration, and increasing the amplitude of the vibration requires additional quanta of that vibration mode. The amplitude of the spin wave is an integer number of of these quanta.

How much energy is this minimum energy? A ferromagnet (like your refrigerator magnets) is a material whose atoms' magnetic moments tend to align so that there is a net magnetic moment of the material. The minimum energy of a spin wave is exactly the amount of energy required to take one of these aligned moments and flip it 180 degrees. If you flip a spin like this, it can propagate through the material by successive mutual flips between neighbors. And we can examine the behavior of these spin flips, and their interactions with defects and oscillations

The spin wave and spin flip are two aspects of the same thing: a magnon.

This is the kind of quantum mechanical dualism you're used to, but it also shows the dualism between particle and field. The spin wave is an excitation over the entire field of atomic spins and the particle is an excitation at a single point, and depending on what we're investigating at the time.

This is how I still envision fields.

The difference between this and fundamental fields is that there's no substrate for the quantum field. There is no aether serving the role of the electromagnetic field that has some property that we excite electromagnetic waves in, and whose interactions with electrons are particulate photons. There is just the electromagnetic field. The same is true of the gluon field and weak fields. However just as water waves give you an analogy for water waves, the atoms in a material give you an idea about how a field works.

And it's more than a simple analogy. Many of the big "verifications" of high energy theorists that we've seen in recent years, Dirac and Majorana fermions, for example, are coming out of materials and metamaterials research in condensed matter. Experimentalists can construct systems with the correct symmetries to realize the particles. It's like creating universes on demand, universes that contain the thins you want to find.

In material, it's even easy to see something that becomes difficult to envision: how do these (at least) 25 fundamental fields of the standard model superpose over the entire universe? In our crystal lattice, quasiparticle fields correspond to different properties of the atomic and material structure. Lattice vibrations become phonons. Magnetic exicitations are magnons. And there are many others, but they all have this character of being related to properties of the collective properties of the material.

You can view string theory in a similar way: there is this fundamental structure of the string, and the 25 fields are all different manifestations of the properties of the string. Is it open or closed? How does it vibrate? In string theory there is just one kind of thing, the string, and since the different manifestations of this kind of string are all conceptualized as excitations in universal fields. So, there may be only a single, universal field.

Both of these interpretations, every particle is a string or every particle is an excitation in the stringy field, would count as Aristotle's "one principle."* String theory is a monist theory, the kind that Aristotle tries to disprove here. I don't think that the arguments he propounded in Physics I.2 really refute string theory, partly because many of them are arguments against specific philosophers and partly because many of them have mistaken logic of Greek mathematics.

For example, if I change a line in Physics I.2 to read "if there is a continuous fundamental field, then immediately it must be many fields because anything continuous must be divisible," then we have string theory exactly as I described it. But, string theory is logically consistent. It is also logically coherent. There is no obvious logical problem with string theory as mathematics. It's only possible problem is correspondence: even though it's currently the best guess at a unified theory of the world, it may never be shown to actually predict anything. But although string theory might not be correct, and there may even be no theory of everything,(*3) the field theoretic structure has both the continuity (say, the electromagnetic field) and the divisibility (say, the photon) built in. In some way. And in some way, it is a counterexample to Aristotle's assertions against monism in Physics I.2.

So, it seems to me, string theory refutes these assertions by Aristotle.

Monism is at least possible.

_____________________________________
* In the translation the, Aristotle is arguing against the idea that there is only one "principle," whether that principle is "a substance, a quantity, or a quality." Democritus has an "infinite number of principles," because his atomic theory had atoms of "all shapes" -- and there are no limits on the number of shapes there could be (If I recall, Epicurus would have a limited number in the form of regular polygons, when he finally got around to being born, if I recall). Heraclitus, apparently, had zero principles. So the wording here made life difficult for me: I wanted a principle to be something like Newton's Law, rather than a substance like water or air.

** I think. There probably should be a quantum mechanical description of transverse mechanical waves on strings, although I don't know what its use would be, or how you'd do an experiment to detect it.

This would be like building up the vibration of a guitar string by adding transverse vibrations to individual atoms, one at a time. That would probably make them phonons.

(*3) Although I should go through these arguments on the TOE page for Wikipedia before I say that.

---

← Previous ( Physics I.1 )

Answering Aristotle

( Physics I.3 ) Next →